| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 경제
- 파이썬
- Linux
- 러닝 스칼라
- Shellcode
- hackerschool
- Python
- backend
- Scala
- 러닝스칼라
- flask
- c++
- hacking
- Javascript
- c
- mysql
- 백엔드
- 리눅스
- 딥러닝
- 웹해킹
- php
- BOF 원정대
- BOF
- webhacking
- Web
- hackthissite
- 인공지능
- 챗GPT
- deep learning
- ChatGPT
- Today
- Total
jam 블로그
Artificial Neural Network 1 본문
신경망 (Artificial Neural Network, ANN)
스터디 용으로 Deep Learning from Scratch 2 책을 참고로 정리한 것입니다.
신경망을 알기 전에 기본이 되는 퍼셉트론(Perceptron)을 먼저 알아봅시다.
단층 퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력.
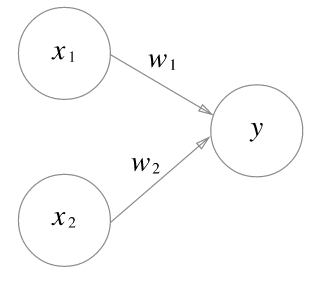
위 그림에서 원은 뉴런 혹은 노드라고 하며, 입력 신호가 y 뉴런에 보내질 때는 각 고유한 가중치가 곱해집니다.
뉴런에서 보내온 신호의 총합이 정해진 한계를 너어선 때만 1을 출력합니다. 다음과 같이 수식으로 나타낼 수 있습니다.
$$
y =
\begin{cases}
0 & (w_1x_1 + w_2x_2 \leq \theta) \\\\
1 & (w_1x_1 + w_2x_2 > \theta)
\end{cases}
$$
단점은 직선 하나로 나눈 영역만 표현이 가능하기 때문에 한계가 존재합니다.
그래서 다층 퍼셉트론을 사용하여 비선형 영역도 표현할 수 있습니다.
다층 퍼셉트론으로 복잡한 처리도 가능하긴 하나 가중치를 설정하는 작업은 수동으로 해야한다는 겁니다. 이를 해결하기 위한 방법으로 신경망이 나옵니다.
신경망은 다음과 같이 구현합니다.

- 입력층 (Input layer)
- 은닉층 (Hidden layer)
- 출력층 (Output layer)
이전과 같이 원은 뉴런이며, 화살표에는 가중치가 존재합니다.
가중치와 뉴런읜 값을 각각 곱해서 그 합에 활성화 함수(activation function)을 적용한 값이 다음 뉴런의 입력이 됩니다.
이때, 각 층에서는 이전 뉴런의 값에 영향 받지 않는 편향(bias)를 더합니다.
입력 -> 은닉층으로 가는 수식을 다음과 같이 쓸 수 있습니다.
$$
\mathbf{h = xW + b}
$$
위 공식을 python으로 나타내면 다음과 같습니다.
import numpy as np
W1 = np.random.randn(2, 4) # 가중치
b1 = np.random.randn(4) # 편향
x = np.random.randn(10 , 2) # 입력
h = np.matmul(x, W1) + b1위 수식이나 코드를 보면 선형 변환이기 때문에 우리가 원하는 비선형 효과를 부여하는 활성화 함수(activation function)을 적용합니다.
활성화 함수 종류는 다양하지만 그중 가장 기본적인 시그모이드 함수(sigmoid function)을 사용합니다. 수식은 다음과 같습니다.
$$
\sigma(x) = \frac{1}{1 + exp(-x)}
$$
def sigmoid(x):
return 1 / (1 + exp(-x))이제 앞에서 입력 -> 은닉층 코드와 시그모이드 함수를 사용하여 출력층을 얻어봅시다.
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.random.randn(10, 2)
W1 = np.random.randn(2, 4)
b1 = np.random.randn(4)
h = np.matmul(x, W1) + b1
sig = sigmoid(h)
W2 = np.random.randn(2, 4)
b2 = np.random.randn(4)
o = np.matmul(sig, W2) + b2아래는 코드는 계층을 클래스화 하고 순전파(forward propagation)를 구현 한 것입니다.
- 순전파(forward propagation) : 입력층에서 출력층 방향으로 처리 결과를 차례로 전파
- 역전파(backward propagation) : 순전파와 다르게 반대로 데이터(기울기)를 출력층에서 입력층 방향으로 전파
import numpy as np
class Sigmoid:
def __init__(self):
self.params = []
def forward(self, x):
return 1 / (1 + np.exp(-x))
class FCL:
def __init__(self, W, b):
self.params= [W, b] # 초기화 시 가중치, 편향을 인자값을 받음
def forward(self, x):
W, b = self.params
out = np.matmul(x, W) + b
return out
class TwoLayerNet:
def __init__(self, input_size, hidden_size, output_size):
I, H, O = input_size, hidden_size, output_size
W1 = np.random.randn(I, H)
b1 = np.random.randn(H)
W2 = np.random.randn(H, O)
b2 = np.random.randn(O)
self.layers = [
FCL(W1, b1),
Sigmoid(),
FCL(W2, b2)
]
self.params = []
for layer in self.layers:
self.params += layer.params
def predict(self, x):
for layer in self.layers:
x = layer.forward(x)
return x
if __name__ == "__main__":
x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
print(s)
'''
[[-1.16143457 0.39407836 0.41527309]
[-1.19352383 0.294051 0.71712765]
[-1.08156366 0.31475275 0.7229573 ]
[-1.72826089 0.34256826 0.24287259]
[-0.46915794 0.55220402 0.62959216]
[-0.99270386 0.34710485 0.73347883]
[-1.38121781 0.31283001 0.58169354]
[-0.93040429 0.42209223 0.57296642]
[-1.5985504 0.2492377 0.53501795]
[-1.34670998 0.30069535 0.62838406]]
''''인공지능' 카테고리의 다른 글
| DIALOGPT : Large-Scale Generative Pre-training for Conversational Response Generation (0) | 2020.03.31 |
|---|---|
| Extreme Language Model Compression with Optimal Subwords and Shared Projections (0) | 2019.12.18 |
| Deep learning natural language processing nlp 1 (0) | 2019.10.20 |
| Deep learning one hot encoding (0) | 2019.10.20 |
| Artificial Neural Network 2 (0) | 2019.10.20 |
